05 May 2014
I threw together a
CFDG
inspired library for Racket, which
I named Deep Mirror.
CFDG popped up in maybe 2004? 2003? Somewhere back there. I played
with it some initially, then played with it again when the guys at
Context Free Art made a version with
a nice GUI.
Short version is, you write a bunch of rules which behave as a generative
context free grammar. Various terminals in the grammar result in image
elements being created, and annotations on terminals (and nonterminals)
result in the state of the drawing system being altered. If you want to
make images out of recursive elements, this is a pretty good way to go.
I made some
pictures
with it, but the version of the language out then didn’t allow you to
write functions, or, as I recall, perform any arithmetic at all. People
did some neat things, and made some attractive art, but I got bored.
the new thing
For whatever reason, it popped back up in my mind this week, and I
thought I’d try and stuff something like CFDGs into Racket, while
leaving you the full power of Racket. I wonder what else I might’ve
concocted if I’d had the entirety of the math
library available
to me back then.
Look at
that, it makes pictures. (code
here)
And that picture right there is an example of why I made this, and why
I'm not quite done with it. See how the red tentacle thing is covered
up by the purple? The recursion is being done depth-first and the red
tentacle is completely drawn before the purple one starts.
I arranged my library to behave a bit differently from the other
tools. Instead of applying arguments to the various rules/shapes, they
just inherit whatever the current drawing state is, sort of like
OpenGL.
You can only multiply new transformations
(x, rotate, sheary, etc) into
the current transformation matrix; no forcing the rotation or
translation to specific values. But the hue, saturation, brightness
and alpha can all be set to a specific value (with hue=,
brightness=, etc), or you can multiply the existing value
by a new one (with saturation, alpha, etc).
The state gets pushed and popped onto a stack, either with the
scope macro, or by calling a rule. scope
is convenient when a rule is going to branch, and you want to define
the changes for each branch in terms of your rule’s starting state,
rather than defining the second branch’s state in terms of the first’s.
next?
Please note! I’d be happy to take pull
requests for
this stuff, or anything else that would be neat.
I want to get some continuation manipulation stuff going to rearrange
the order in which evaluation occurs. First (read: simplest) I want to
change the recursion to be breadth first, instead of depth first.
That’d take care of my tentacle problem above.
Second, I’d like to experiment with rearranging evaluation so that the
scale of the current transformation matrix is used to reorder all the
outstanding rules from largest to smallest. Or vice versa. Keeping an
eye on the current scale would also let me cut off recursion
sooner. Once you’re down to drawing subpixel elements… well. You’d
have a lot of work to do to influence the final output.
Third, I’m hoping that while playing with these static alterations to
control flow, I might come up with some neat way for the user to
specify control flow, which fits with the style of CFDGs.
I’d also like to fiddle with the
parameterization
of the state. I’m a little worried that what I’m doing to keep the
state hidden in the background is doing tragic things to the performance.
Oh! Layers, so you can manipulate the z-index. Which would be
another way of getting my uncooperative tentacles arranged neatly.
02 May 2014
Normally I don’t even look at things with titles of the form /Sucks$/.
I clicked on this expecting something obnoxious that would upset me
enough get the blood flowing, and wake me up. Instead I laughed hard
enough to wake up.
I appreciate the part about the bridge project; I feel that it conveys a
sense of the way in which software developers make their own projects
more miserable. The line or two about Phil are the only ones that
touch on the expectations of others, though.
I think that most of the people who purchase bridges have a sense that
certain design requests become unreasonable once construction has begun.
And that asking for a bridge twice as big is going to at least double
your materials costs.
Unfortunately software developers don’t get the same consideration.
I’m not sure I know why. (Not that there necessarily has to be a
single reason.) Perhaps those commissioning us to develop software on
their behavior are so in awe of our ability to build castles in the
air (see below) that they assume we can accomplish anything. That’s
certainly a much more pleasant possibility than the one normally
bandied about.
This one is a response, at least in part, to “Programming Sucks”. I
feel it takes “Programming Sucks” a bit too seriously (or maybe
literally). I see “Programming Sucks” not as a complaint, but rather
an attempt to explain some negative aspects of programming as an
activity, which non-programmers probably have no inkling of. This
piece then comes along an attempts to explain positive aspects of
programming, which non-programmers probably have no inkling of.
I feel it is worth pointing out that you can have aspects of an
activity which you don’t enjoy, while still very much enjoying the
activity overall. Hikers don’t like bad weather, but you deal with
a bit of that in exchange for the good weather. Fencers don’t enjoy
being hit by their opponents, but the winning (or at least interplay
that happens before losing), makes it worthwhile.
Building castles in the air is worth it, even if Phil makes us leave
the railings off all the parapets.
28 Apr 2014
The
ReCode Project popped up in 2012,
with the neat goal of taking old computer art, and writing new
programs (in
processing) that
regenerate the art, or close approximations. This is made tricky
enough by the lack of source code, and little to no description of the
algorithm(s) used.
To make it slightly more challenging, the original material looks
like it was run through a cheap photocopier a couple of times. Weee.
I came across a link to the project... hm, who knows. Probably some
awful site with lots of comments. I hadn't done any work with
processing at that point. Obviously the thing to do was
participate.
I think the art on there can be placed along a sort of "pain in the ass"
gradient, from most to least:
That's just an excerpt, the original doesn't have the nice square
aspect ratio. If you decide to snarf the PDF so you can see the
original, head's up: it is 20.2MiB.
I looked at it for awhile, screwed around some, probably did a little
bit of whatever I was supposed to be doing. Stuff 'n things.
the process
When I look at that I see a circle, with 270° arcs on either side
of it. Hm, nope, I see three arcs. 270°, 360°, 270°. That's easier
to deal with.

Then a half-circle has been extruded along the lengths of
the arcs, producing a 3D volume. We could stop there, and feed that
into a ray tracer, and have a nice "realistic" looking image.

Yeah, about like that! Who doesn't like some nice perfectly smooth
jade floating above an infinite checkboard? If you'd like to enjoy
some 90's POV-Ray flashbacks, you can play with the
source for that image, too.
We've got some nice geometry now, but the general appearance isn't
even close. Ray tracing clearly wasn't used. In fact, if you look at
the inside of circle, near the bottom, I think it is clear that no
hidden surface removal was performed. My assumption, and what
I went with in my version, is that it is just made up
of some lines being drawn in 3D space. The renderer doesn't have
any idea that it is depicting solid surfaces.
At this point, you might want to reference
my code. I started with the RaisedArc class, which
represents the arc segments, and computes their height. Just some
trig going on there. Take a point, figure out how high that arc is
at that point.
The draw function can then just drag a "pen" across
the X-Y plane, stopping along the way and asking each arc how high it
is. Take the max, and you reconstruct the surface of the object we
rendered:
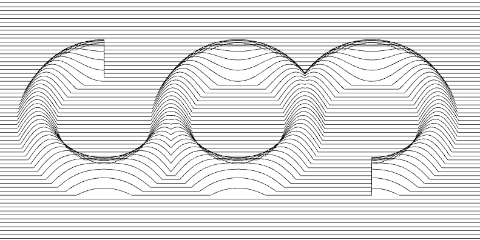
When I hit that, I felt that my decisions up to this point were
justified. This felt like the same image, and maybe it is even what
the original artist would've wanted to make if they'd had anything
close to EGA
resolution available. But they didn't. So this image is too "nice",
and certainly too smooth. Of particular concern, the truncated ends
of the left and right arcs don't even look right anymore. In the original,
they actually hint at a bit of perspective, even though I believe the
image was rendered orthographically.
"Fixing" the smoothness is taken care of in two steps. First,
we up the step size (fx_step) until the lines are
made of distinct segments. Then noSmooth() turns off
processing's attempts to help us out and make the lines look nicer.
Conveniently, increasing the step sizes makes the truncation of the
arcs much rougher, and gives us the pseudo-perspective appearance.
That's handy because 1) now I don't have to do anything else and 2)
it acts (in my mind) as further evidence that the original was drawn
orthographically instead of in perspective.
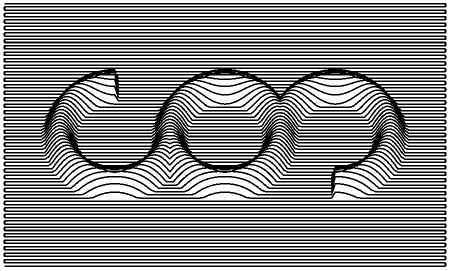
I counted the number of horizontal lines in the original, and sort
of eyeballed the other proportions. The fy-0.5 in the
call to computeHeight is to scoot the geometry around
until the lines appear to be falling across it as they do in the original.
The stroke width, and tilt of the X-Y plane were both determined by
just fiddling around with things. ...I just noticed that the angle I concocted,
of 28.12° is 0.4907 radians. I'm guessing that means the original used
a round 0.5 radians. Maybe I'll change that some time. Ehh.
next?
The same "rendering engine" used for this piece could actually be applied
to the map of the United States referenced above. Clip off stuff outside the
borders, and replaced RaisedArc with something that reads a data
file, and bam. That could be fun.
I'm also tempted to do Roger Coqart's From
the Square Series. It isn't clear to me that there is a pattern in
how the lines are placed, but I think we could get fairly close with some
rules about the distribution of line segments. Perhaps adding them at random
until they get close to satisfying some rules.







